Longest Narrow Path
This is a pentomino problem that I did not think of myself, but which kept me busy nonetheless. I'm not sure who originally thought of the version I was working on, but I'll describe how I came to know it.In late February 2005 I stumbled across the pentomino contest described on another webpage. Actually the problem involves using both pentominoes and tetrominoes (the four shapes each formed with 4 squares). The puzzle is to use the pieces to enclose a "narrow" (single unit width) path of longest length. The path must be closed at both ends, cannot be a loop, have no branches, and must be properly enclosed (no pathway corners touching).
Sometime during the next week I was playing boardgames with some friends. Someone brought out a set of pentominoes and that reminded me on the contest. I could not remember the exact path length given as an example of the contest page, but I knew "it was somewhere in the forties."
What I had completely forgotten was the tetrominoes were used as well. So, while playing Russian Rails over the next few hours, my friends and I tried to enclose the longest path possible. I was stumped by the fact that we were coming nowhere near 40. My friend Robert kicked things off by getting a length of 31.
About an hour later I squeaked out a score of 32, and with half an hour of that I upped my answer to 33.
But I knew the example I had seen was in the 40s.
The 33 was the highest achieved that session, and when I got home I immediately searched for the original webpage again to see what was going on.
Oh... that example used tetrominoes too...
That explained that.
But what about using just pentominoes?
The answer of 33 seems pretty good.
Surely someone has looked into this... and maybe better answers found.
I emailed some friends-in-pentominoes about the question, and by the next morning Aad de Wetering of the Netherlands told me that the best solution he had ever seen was one he had created. It is pictured below and has a path length of 36.
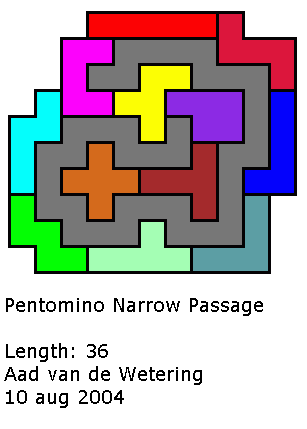
He was pretty sure that no answer above 36 was possible.
36. Wow. Granted, I had only played with the problem a couple of hours the night before, but an improvement of 3 over my best answer certainly impressed me.
That next day I decided to tackle the problem again. Even if I could not get 37 (which had not been formally ruled out yet), I still wanted to see if I could achieve my own configuration for 36 (though it was not even clear that there could be multiple 36 length solutions).
I spent about 7 hours attacking the problem. At my house on the couch. At the local coffeeshop. Back at home at my desk in fromt of my computer. By 10:00 at night I was about ready to concede defeat, when, "eureka!"
I found my own answer for path length of 36:
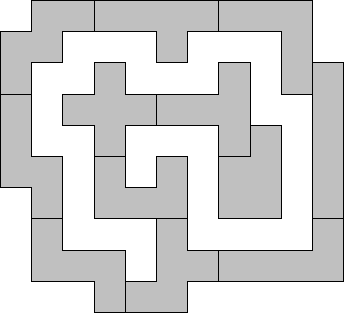
I still don't know if 37 is possible, but I, too, am now highly skeptical.
If anyone finds a better answer, please let me know (or, if you find your own 36 solution, I'll be happy to present that as well).
- Eric Harshbarger, 5 March 2005
Update (12 Mar 2006): Dan Edlefsen contacted me to say that he had found his own 36-length narrow path with pentominoes. He also doubts that a path of length 37 is possible. However, he did pose an additional question. Using two complete sets of pentominoes, what is the longest narrow path that can be form? He has managed a length of 79 but speculates that up to 82 my be possible.
Update (24 Nov 2018): I would still bet against there being a 37-length solution to this problem, but after some recent experimentation, I came very close to just such a goal. In the configuration below the path is 37 units long and the only shortcoming is the absent corner block near the very end (indicated by the red circle). One can see that there are two "unused" units (yellow dots marking them). So there are, theoretically, enough squares to use for the walls. If only one of those extra units could be shifted about to fill that corner...
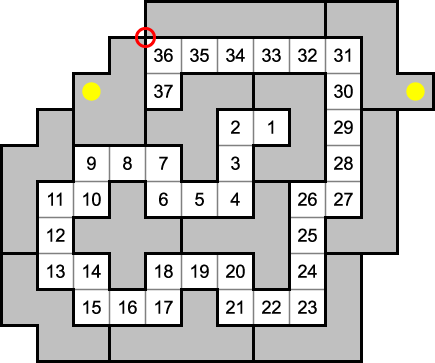
Back to Eric's Pentominoes Page