Landlocked Pentominoes
One of the most common puzzles for the 12 pentomino pieces is to try to arrange them into a 6x10 rectangle. There are 2339 ways to do this. Here is one example:
One will note that in this solution three of the pieces, the T-, W-, and Z- pentominoes, do not touch the edge of the the 6x10 box; they are properly in the interior of the figure. I refer to these pieces as being "landlocked".
I began thinking about this landlocked property, and wondered how the other 2338 solutions compared to this one. Were there any solutions with 4 landlocked pieces? Even 5? and how about at the other extreme: were there any solutions which had only 1 landlocked piece? Or even any with no landlocked pieces whatsoever?
I posed this question to a fellow whom I knew to be a pentomino enthusiast. A short time later this person, Tom Saxton of Idle Loop software answered my question. After some computer analysis on his part, he provided the following information: there are no 6x10 solutions with 5 or more landlocked pieces. Below that number the breakdown is as follows:
LL # of SOLUTIONS -- -------------- 4 207 3 1111 2 864 1 155And, to my surprise, there were some solutions that have NO landlocked pieces, but only a couple. Here is the image Tom sent to me:
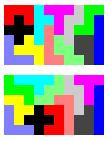
As you can see, in each solution all of the pieces extend out to the edge of the rectangle.
I guess that settles that.
Thanks, Tom.
- Eric Harshbarger, 3 January 2005