Enclosing Extra Pieces

While compiling and inventing designs for the Pentomino Daily Calendar I included twelve configurations which are often thought of as "missing piece" designs.

Since each of the 12 pentominoes is made from 5 squares, any design based upon all of them will be composed of 60 squares. One can concoct designs based on a 5x13 rectangle (65 squares) which has a "hole" in its interior. This hole can take the shape of any of the 12 pentominoes. For example, here is a solvable design, a "missing N" configuration:

I furthered this idea of holes shaped like pieces by using a 7x10 rectangle and including two holes in the interior, each hole the shape of a pentomino (possibly the same shape). For example, a "missing N and Z" form:

It turns out that you can create a solvable configuration consisting of two holes within the interior of a 7x10 box for any piece-shaped holes. When I say "within the interior" I mean it properly: each hole is at least one square away from the edge of the enclosing box, and the two holes do not touch each other, not even at corners.

Including using two holes of the same shape (say two "X" holes) there are 78 different 2-hole combinations.

I included 66 such designs in my Calendar puzzles and then focused on bounding multiple holes of the same shape. Would it be possible, say, to create a rectangle which enclosed three holes each shaped like the "W" piece? What about the other shapes?

One needs a rectangle sized 5x15 (75 squares minus the 15 determining the holes leaves the required 60). No other true rectangle is reasonable (since 75 has no other factors besides: 3*5*5, and obviously a 3x25 rectangle would not work). Unfortunately this rectangle won't do the trick. The I-pentomino is the troublesome piece. There is no way to include three long I-holes in the interior of a 7x15 box so that the configuration is solvable with the 12 pentominoes.

I then decided to modify the bounds a bit. I used a 7x11 box with two opposite corners removed. This, too, failed for the I-holes. So, while I could manage to form "missing triplets" for 11 of the pentominoes in a 7x11 box with opposite corners removed, the I-pentomino once again caused trouble (pictured below is the example of the X-configuration -- for which there is 1 solution).

I did, however, find a bounding design that did allow three I-pentominoes in its interior. It is not quite as aesthetically pleasing as a rectangular box, but it is solvable (there is only a single solution):

Problem was, I could not find a way to enclose three X's in that bounding shape.

So now, the question is posed: Can one find a single bounding shape which can enclose any triplet of pentominoes? I don't know. The I- and X-pentominoes seem to be the troublesome two. If a bounding configuration affords one, it seems to fail on the other. If anyone discovers such a shape, I'd love to see it.

Finally, I also managed to discover figures which enclosed a specific quartet and even quintet. Both cases involve the friendliest of pentominoes: the "P" shaped one. For each design there is only one solution:

I do not know whether quartets or quintets of other shaped pieces may be enclosed. And I conjecture that no sextet of pieces can be enclosed.

- Eric Harshbarger, 2 Jan 2005

Update (14 Jan 2005): Michael Keller and Aad van de Wetering both attacked my triplet question above and within a day of each other sent me emails. The former's included the following kind words:

It's too bad there isn't an annual award for best new pentomino problem. Eric Harshbarger would be my nominee for 2005, even though the year has just begun...

About an hour ago, with the help of Aad van de Wetering's polyomino solver (to quickly test various positions), I found a shape which would work for both I and X. It took 45 minutes or so to find solutions for the other ten pentominoes. For eight of the shapes, the first solvable position I found had a unique solution. LNPU had multiple solutions: 18 for P. With a bit more work, I found hole positions for all 12 which had unique solutions. I attach only one of the 12 solutions, for I-I-I.

If Eric wants to post the solution on his page, he can surely do so. (I can provide all 12 solution diagrams). I would like to include a link from my polyform pages...

Michael Keller
http://home.earthlink.net/~fomalhaut/polyenum.html

Michael Keller's solution

Aad van de Wetering's solution

Update (18 Jan 2005): Michael Keller has been busy. He has now provided me with a "missing quartet" configuration for a shape other than the P-pentomino. Below is one involving the U-.

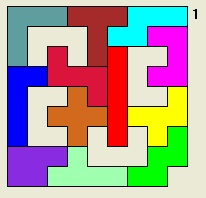
Update (29 Jan 2005): More submissions. The first is from Kate Jones of Kadon Enterprises. She illustrates an enclosure of 5 U-pentominoes:

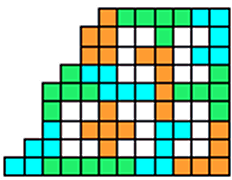
Next, Aad van de Wetering returns with many solutions to 4, 5, and even a 6 enclosure of various pieces:

Back to Eric's Pentominoes Page